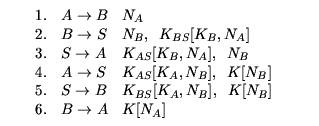
July, 2001.
A method for adapting protocols
Example 1: A mutual authentication and key agreement protocol
Discussion and further research
Back to home page , Back to ISG Home Page
The focus of research in authentication protocols has predominantly been on security. There has not been much work published on the analysis of protocol efficiency. In [1], Li Gong proved lower bounds on the number of messages and the number of rounds for a protocol in a collection of different settings and goals. This serves as a useful reference for system and protocol designers. An example given in the paper is that a protocol version which has more messages and fewer rounds (hence faster to complete) may be suitable in the case where a client needs immediate authentication, while in the situation where the network is unreliable the client may wish to run the version with fewer messages.
There are situations however, where even in an unreliable network, a protocol with fewer but longer messages may not be a good choice. For example, in a channel where errors occur in bursts it may be more efficient to send shorter messages so that on one hand the possibility of errors occuring while transmitting is minimised, and on the other hand if a message has to be sent again at least it is short. In a three-party protocol, the channels available between each pair of the participants may be different. For example, a home user may have a slow link to the service provider, who may have a fast link to a third party. In such situations, a round- or message-optimal version of a protocol may not be the most suitable version.
Here we introduce a framework in which we can investigate the possibility of adapting a security protocol in order to obtain optimal efficiency according to the communication channels available. This method is based on the observation that there is a partial order imposed upon the actions of the various parties involved in a protocol. We define operations permitted on the directed acyclic graph corresponding to the partial order and obtain transformations of the original protocol. Performing these transformations on the protocol we enumerate the options available to a system. We will describe our method in detail in the next section and give two examples to illustrate our method. We also give a brief discussion on the security implication of our transformation.
In an authentication protocol, messages are exchanged between the parties. Some messages must be sent before others. For example, in a handshake, the session key must be received before a handshake message can be sent. Informally a message is made up of components, and a component may be a nonce, a name or an encrypted message. We use the terms messages and components in the sense of [2], where the set of messages (called terms) are generated from two disjoint sets, the set T representing texts such as nonces or names, and the set K representing keys, by means of concatenation and encryption. A component is defined to be a term which is not a concatenation of terms. We define an action then to be the sending of a component from one party to another.
We may view these actions and the order imposed on them as a partially ordered set A with a strict partial order ``<'' defined as follows:
There is a directed acyclic graph G(A) corresponding to the partially ordered set A (see [3]): the vertices are the elements of A and there is a directed edge from y to x if and only if x < y. A partially ordered set may also be represented using a Hasse diagram, which is a graph with vertices corresponding to elements of the partially ordered set, and the points x, y are joined by an edge with x ``below'' y if and only if x < y and there are no points ``in between''. We will also label a vertex (A,B) if it corresponds to a message sent from A to B.
Now, we define operations on vertices and edges corresponding to the merging of messages and the forwarding of a message via a third party:
We perform the operations on the graph until we obtain a chain. This chain will correspond to a protocol, which can then be analysed for its suitability to the communication channels available to the system.
We illustrate our ideas with two examples in the next two sections.
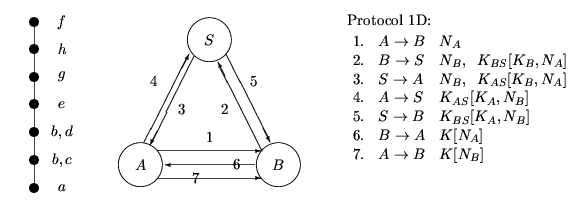
This is a message-optimal protocol given by Li Gong in [1] to demonstrate the achievability of the lower bound for mutual authentication and key agreement with joint key control. There are three parties involved, A and B achieve mutual authentication and agree on a session key with the online help of a trusted server S.
We assume that
We use K[m] to denote encrypting m using the key K, and we use NX to denote a nonce generated by X.
The protocol is as follows:
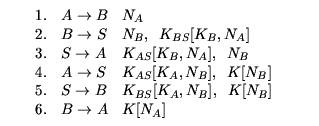
The partially ordered set {a, ... , h} and Hasse diagram associated with this protocol is as below:
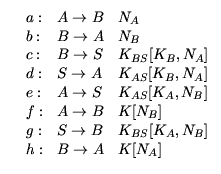
| a < c, | a < h, | b < e, | b < f, |
| c < d, | d < f, | e < g, | g < h. |
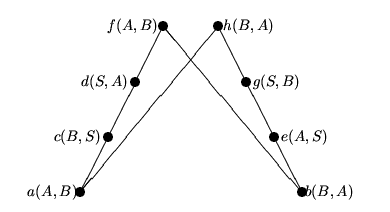
Since we assume that A initiates the protocol, we must have element a of the poset as the minimum element. Hence we have an addition relation a < b. The only possible operations on the poset therefore are
Merging c with b and e we obtain the following:
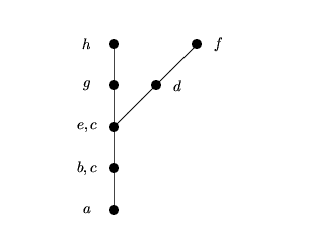
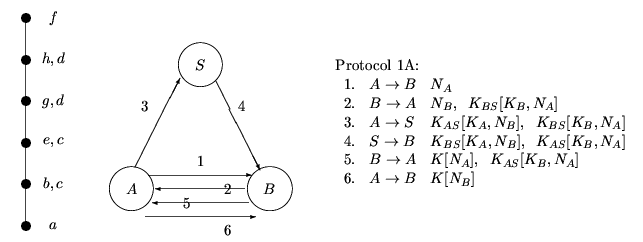
There are two possible ways to proceed from here: merge d with g and h or merge g with d and f. The first possibility, merging d with g and h gives the following:
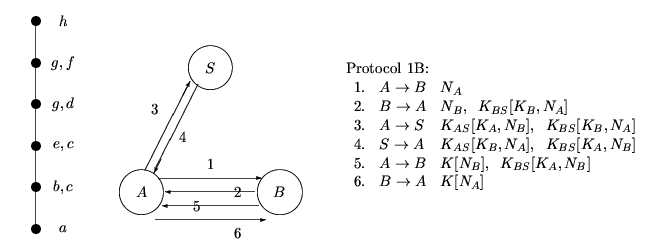
The second possibility, merging g with d and f, gives us the following:
The only remaining possibility arises from merging f with e and g, b with c and d, in either order. This in fact gives the original protocol.
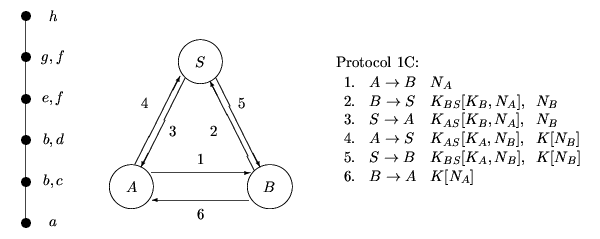
Hence we see a message-optimal protocol may be adapted to suit different communication model. In a situation where we want to spread the communication load evenly between the channels, we may choose Protocol 1C. If the channel between B and S is very slow we may use Protocol 1B, while if we want to minimise communication between A and S, and between B and S we may choose Protocol 1A.
Other possibilities exist if we add new relations before merging, among them the following:
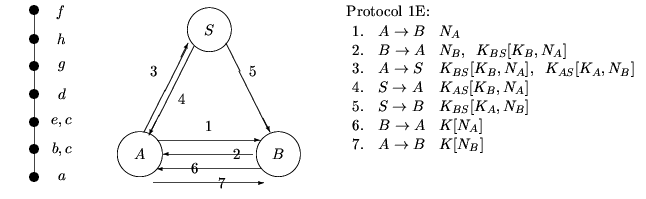
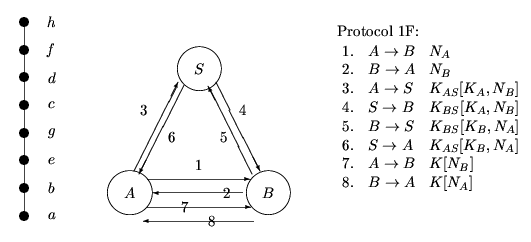
These protocols have more shorter messages and may suit channels where retransmission is frequent.
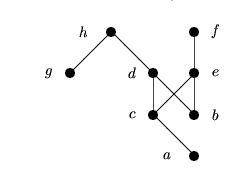
This is the protocol given in [2] as an example of a design process which concentrates on the authentication tests proposed in the paper. There are three parties involved, A and B achieves mutual authentication. The session key K established between A and B is generated by a trusted server S, who shares a secret key KA with A and a secret key KB with B. We use the same notation as the previous example for encryptions and nonces. The protocol is as follows:
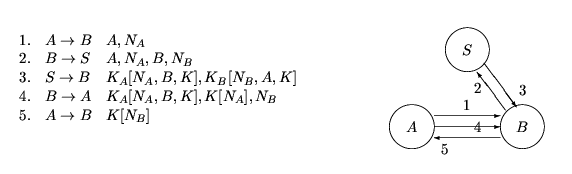
The partially ordered set {a, ... , h} and the Hasse diagram associated with this protocol is as below:
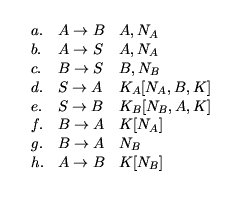 | 
|
We assume that A initiates the protocol, hence either a or b must be the minimum element. The only possible operations on the poset are
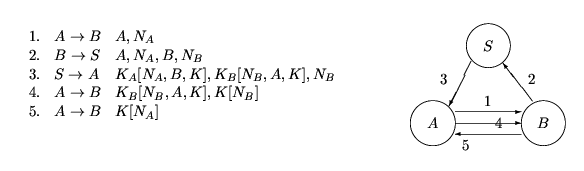
We discuss briefly what we achieved in this work so far and identify further research areas:
We do not claim that the security of a protocol is preserved under the transformations we proposed. As mentioned before, we are primarily interested in communication efficiency. The security of the resulting protocols should be analysed individually. However, consider the strand space model for analysing protocol security ([2]). The analysis in this model depends entirely on components of messages sent within a protocol and their relative order within the protocol. In our transformations we preserve these. Hence it is likely that a protocol resulting from our transformation will satisfy the same authentication theorems satisfied by the original protocol. In fact, it can be shown that the second protocol of Example 2 satisfies the same authentication theorems as the original protocol. We will examine whether this is true in general in the next stage of our research.
We have given a framework in which to analyse the possibility of adapting a given protocol to suit a specific communication channel. We are however not advocating switching between the various protocols according to the behaviour of the network at the time. For example, if the channel between B and S is down we might choose to use the version 1B of the protocol in Example 1 which does not require communication between Band S. Such flexibility would seem to be practical in the less-than-ideal world of communication networks. However it is not clear if this lays the system open to attacks by penetrators interleaving different versions of a protocol. More work is needed in this area of mixing protocols.
There are possible extensions to our method. In this document we have only concentrated on one level, that is, we dealt with only the higher level of sending and receiving messages rather than the computational level. We could extend the definition of an action to include things like generating a random number, encrypting or decrypting a message as well as sending a message. This may help us in identifying critical actions, and in deciding whether to generate and store items, or generate at the last minute before sending, according to what sort of device one has. On the other hand, we could assign weights on actions which depends on the components or the channels (the labels), for example, a weight could be a pair (time, money). We may then choose a protocol that is optimal according to our measure.
[1] L. Gong. Lower Bounds on Messages and Rounds for Network Authentication Protocols. In Proceedings of the 1st ACM Conference on Computer and Communications Security, pages 26-37, Fairfax, Virginia, November 1993.
[2] J. D. Guttman and F. J. Thayer Fábrega. Authentication Tests. In Proceedings of the IEEE Symposium on Security and Privacy, May 2000, IEEE Computer Society Press.
[3] O. Ore. Theory of graphs. American Mathematical Society, Providence, third printing, 1967.